鯵坂もっちょさんはブログの記事ごとに1つ、わかりやすい図やGIFアニメを使って数学のさまざまな概念を解説しています。それらの記事ははてなブックマークでも人気を集め、「内容がわからなくても面白い」というコメントも。
鯵坂もっちょさんが「数学ブログ」を続けるモチベーションはどのようなものか、そして書き始めた理由について、寄稿していただきました。

鯵坂もっちょです。「ブログを書くこと」について何か書いてください、とのことです。
ではここでそれを完全に無視して素因数分解の一意性について説明しましょう。とかやったら怒られるかな。怒られるよな。
でも数学系の界隈ってそういうことをやっちゃう人、結構いそうではある。
……やめよっかこの話。
私について
「アジマティクス」というおもしろ数学つまみ食いブログをやっています(「おもしろ」は「数学」を修飾しています)。
どんな感じはこの先を読んでいただければわかるとして、とりあえずここでは複素数の掛け算をご覧ください。
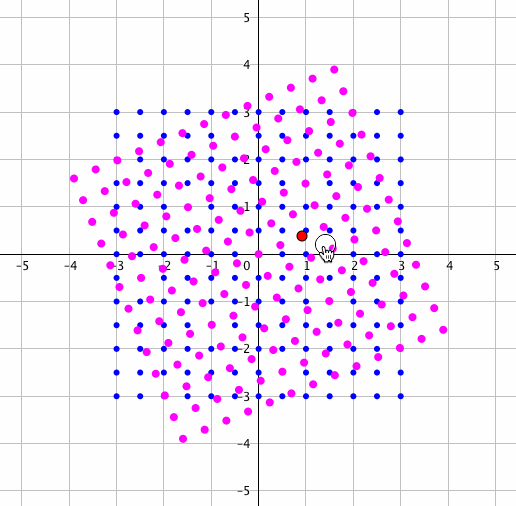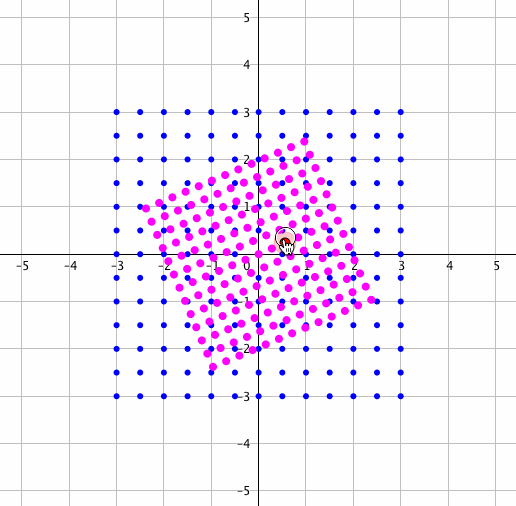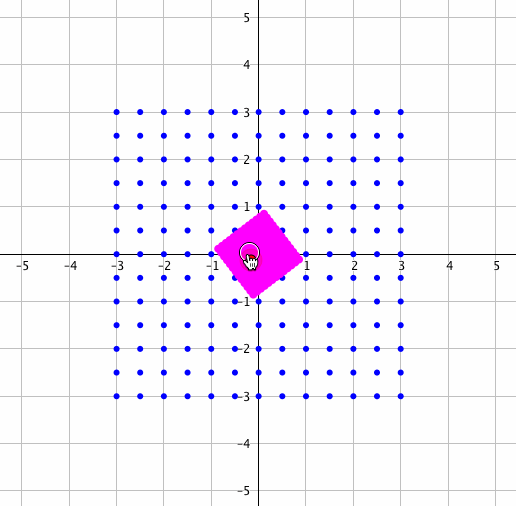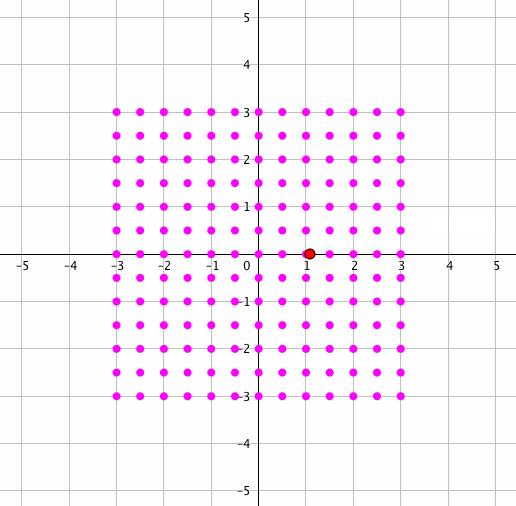
いいですね〜
「ブログを書くことについて」と言っても、このブログは基本的には「一記事ごとに一つ、数学の概念を解説する」スタイルなので、「ブログ」という言葉から想像されるものとは少しズレているかもしれません。
つまりは「日記」ではありません。なのでこのブログには自分自身のことについてはほとんど書いていないんですね。
まあそりゃそうです。数学の面白いところが知りたくてやってきた人は「鯵坂もっちょ」に興味がありません。
「誰々が言ってたから正しい/間違い」が存在しないのが数学のいいところの一つですが、とはいえ中にはそういう判断をしてしまう人もいるでしょう。
そういう理由もあって、私は私のことについてアジマティクスにほとんど書いていません。誰が書いたかで判断されたくないので、という思いもあるんでしょうね。知らんけど。
ただ、他の数学ブログと比べるとけっこう日記っぽい記事もあるのがアジマティクスの特徴とも言えます。
「ハワイに旅行して海がきれいだったので水平線までの距離を計算してみた」や「ルービックキューブができなすぎて悔しいのでその構造を考えてみた」のような現実世界との関わりを多めにやっていて、それらは他の数学ブログにはあまり見られない要素なのではないかな、と思います。
そんな感じでやっている人です。自己紹介でこれ以上何か言うことある? 既婚です。まだ手足をジタバタさせることしかできない元気いっぱいの双子の0歳男児に乳首をバカスカ殴られ股間をバカスカ蹴られています。助けてくれ。
ブログを書く理由
さて。
鯵坂もっちょさんがブログというものを書く理由について聞かせてほしい、とのことで考えてみましたが、おおまかに4つあることに気づきました。
そのうち1つはかなりきれいな理由。1つは普通にきれいな理由。もう1つはまあまあきれいな理由。残り1つは、あまりきれいではない理由です。
「きれい」ってどういうことを言っているのかは、たぶん読めばわかります。
理由1(かなりきれい)
ブログを書く理由の1つ目は、文章としてアウトプットしたほうが自分の理解が深まるから、です。きれいですね。
これは「何かを説明する、解説する、わかりやすく伝える」ということに挑戦したことのある人なら総じて心当たりのある話なのではないかと思います。
「数学の解説ブログ」などと標榜しているからにはある程度、そのとき扱おうとしている概念(概念Aとします)をわかりやすくかみ砕いて伝えることができなければなりません。
そして、概念Aをわかりやすくかみ砕いて伝えられるようになるためには、自分の中で概念Aがある程度かみ砕かれた形で理解されていなければなりません。
ということで、「ブログを書くために」というモチベーションでもって概念Aを理解しようと頑張る、という行動が発生するのですね。
まあ普段ボーッと生きてても「よし、中国剰余定理を理解しよう」ということにはなりませんから、こうやってモチベーションが外部から与えられるのはとても助かることです。
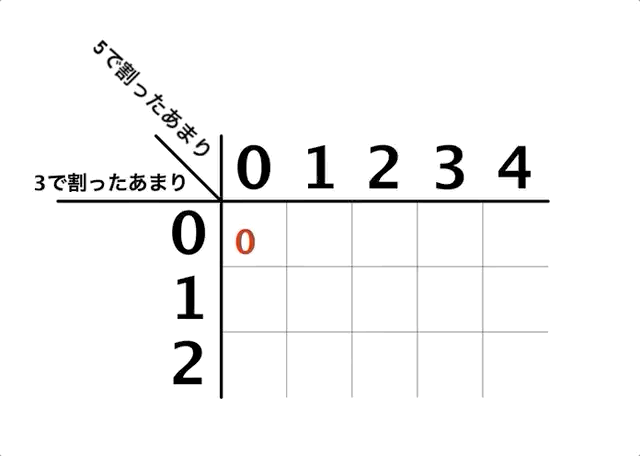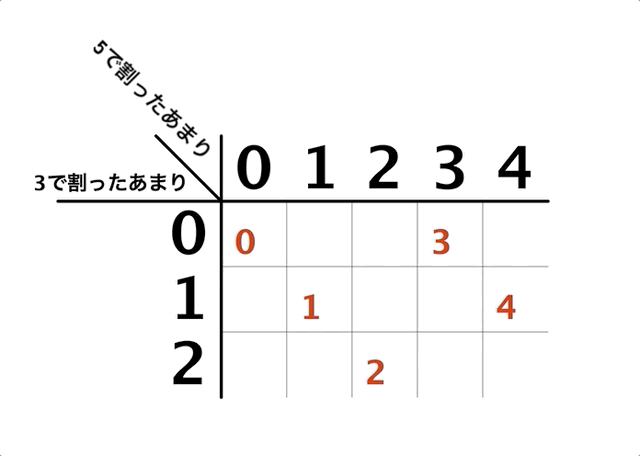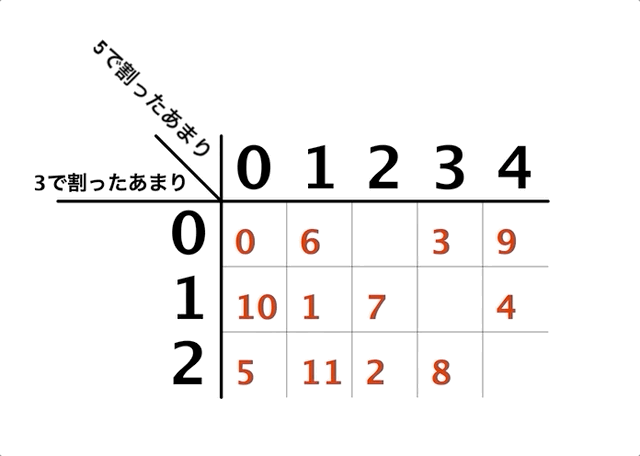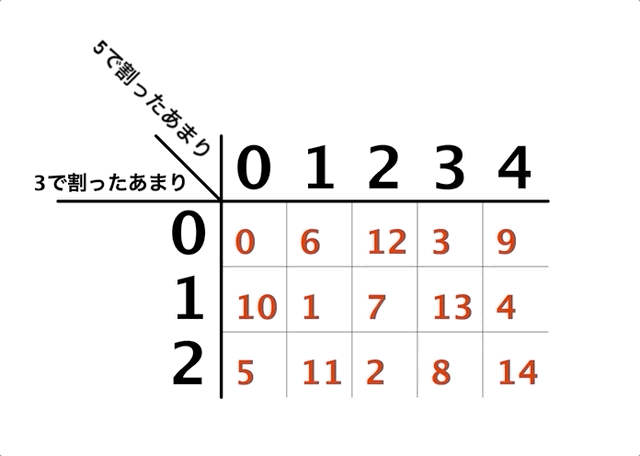
中国剰余定理
そしてこれは大いに「ブログを書く」ということの理由にもなり得るんですね。
なので、あまり大きな声では言えませんが、ブログを書き始める段階ではあまりちゃんと理解していなかった、ということすらあるんですね。
この辺のことはあんまり理解してないけど書き進めてるうちに必要に応じて理解してくるやろ、と未来の自分を信用しているわけです。
「明日の自分に任せて今日は寝よう」みたいな話ですね。死亡フラグやん
もちろん、これはあまりおすすめできるやり方ではありません。書き進めても結局理解が及ばなかった場合、その記事はボツになることが多いです。
私の下書き欄にはそのようないきさつでボツになった記事たちの怨念が渦巻いています。
でもこのやり方にはいい面もあって、「とりあえず書き始めることができる」んですね。逆に「ちゃんと理解してから書き始めよう」と思っているといつまで経っても書き始められません。
数学に限らない話だとは思いますが、一つのことを理解すると、それを足掛かりにすることができるようになり、そしてそれを足掛かりにしないと見えてこなかった問題意識を抱けるようになります。そうすると今度は、その問題をちゃんと理解してから書き始めよう……と思うようになり、以下無限ループです。
どこかで割り切ってエイヤで書き始めることも大切なのだと思います。怨念たちには悪いですが。
理由2(普通にきれい)
2つ目のきれいな理由は、数学の面白い話を知ったらみんなに伝えたくなっちゃうから、というものです。
2017年から「数学デー」という名前のイベントを運営しています。数学好きとかそうじゃない人とかが集まって、数学について話したり問題を解いたりゲームしたりするイベントです。
詳しくはこちら↓
数学デーではさまざまな話題が出ます。当然、私の知らない話もたくさん出るわけで、その中で抱く「これは面白い!」という感情は「ブログに書こうかな」に直結しています。
例えば以下の記事なんかがそうです。これらの記事ではこの話を知ったときの興奮がそのまま文章にされています。
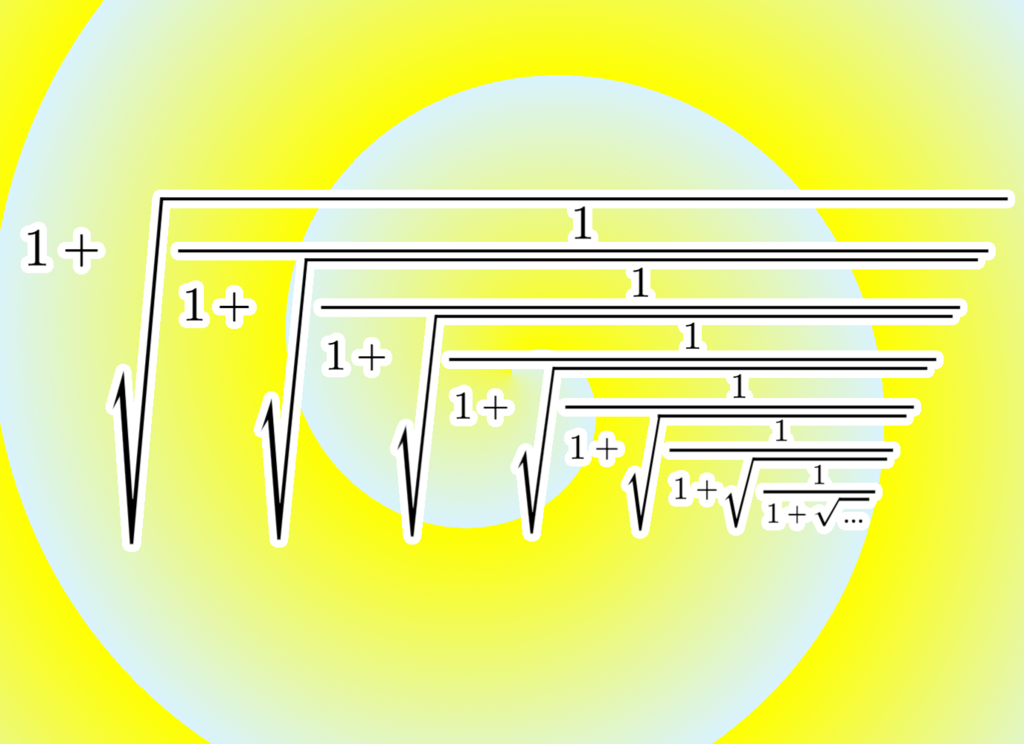
やばい連分数
ていうか書いとかないと忘れるしね。
どれだけ面白くて興奮した話であっても、書いておかないと必ず忘れます。書いても忘れます。
ときにはダラダラと1ヶ月くらいかけて書いていることもあるのに、それでも忘れるんですね。
でも書いてあればいつでも思い出せます。
理由3(まあまあきれい)
3つ目の理由は、ググって出てくるような数学解説は初学者を突き放していることが多いから、もっとストレートに言うならそういう解説記事は大概わかりにくいから、というものです。
つまり、そういうものが多いので、それなら俺がもっとわかりやすい解説やったろうやないか、と腕まくりをしているわけです。
例えば「行列式」について、Wikipediaの冒頭ではこんな書かれ方になっています(以下は例として挙げただけであり、内容を理解しようとする必要はありません)。
どう思いますか? これ。
多くの読者には「わかりにくい」「何を言ってるのかわからない」という感想になるのではないかと思います。特に「行列式」ってなんだかよくわからないけど、よく耳にするからどういうものかだけでも触れておきたいなぁ〜、くらいの人にとっては。
そういうことではないのですね。Wikipediaの記述が悪いと言っているのではない。つまりは対象読者が違うのです。
このWikipediaの記述は明らかに「行列式をすでに知っている人」に向けて書かれています。
ところが、行列式を知っている人だけが「行列式」と検索するのかといえば、当然そうではありません。それこそ上述のようになんとなく知っときたい、くらいの人も少なくないはずです。
2016年にアジマティクスを始めた当初は、そういう人たちの受け皿になるくらいのレベルの数学記事がネット上には本当に少なかったのですね(今だと数学系YouTuberの方なども多いのでだいぶ状況も良くなってきてはいるように感じます)。
それが3つ目の私がブログを書く理由、もとい、これに関しては書き始めた理由でもあります。
一度、読者の方から「数学用語で検索した結果の一番上が全部アジマティクスになればいいのに」といううれしい反応をいただいたことがあります。
それはさすがに大きすぎる目標かもしれませんが、心意気としてはそんな感じになれたらいいなあ、くらいでやっております。
「行列式」という言葉が気になった方は、以下をご参照いただければ楽しいと思います。
理由4(決してきれいではない)
最後の理由は、まあ、なんというか、こんなこと言うのも本当にアレなんですが、承認欲求です。
私は数学解説ブログを書く者として、「わかりやすく物事を伝える」ということに関してはいっぱしの自信があります。
単純に「これをどう書けばわかりやすくなるだろうか」と知恵を絞ること自体が好きだったりもします。
そしてありがたいことに、記事を読んで「わかりやすい」という反応をいただくことも珍しくありません。本当にありがたいことです。
これが、美味いのですね。
いや本当に。おいしいおいしい。いくら食べてもお腹いっぱいにならない。
これはもうほとんど麻薬です。
最近ちょっと承認欲求切れてきたしアジマティクスでも一本キメとこうかな、みたいな。
ね。きれいじゃないでしょ。
「ブログを書く理由」として、大手を振って答えられる回答ではない。
「あなたがブログを書く理由を教えてください」→「承認欲求を満たすためです」って、ちょっと、ねえ。いや、でも逆に大物っぽいな。俺大物かもしれん
もちろん、これはどちらかといえば些末な理由であって、ブログを書く理由として大きいのは理由1と2と3です。
まず数学の面白い話を知り(理由2)、でも知ったばかりであまり深く理解できてはないので理解しようと頑張り(理由1)、調べてみると案の定巷間には初学者にやさしくない記述が多いのでじゃあ俺がいっちょやったろうかと筆を執る(理由3)。
こんな流れであることが多いですね。もうこの時点でいろいろな目的は達成されているので、承認欲求に関しては、満たされようが満たされなかろうが別にいいかなといったところです。満たされたらそれはそれでラッキーだね、くらいのもので。
承認欲求が第一の理由になってしまってはまずいと思っています。書いた記事があまり読まれなかったというだけでブログを書くモチベーションを失ってしまうことになりかねません。
もし承認欲求がブログを書く最大の理由になっていたとしたら、1年も持たずに私はブログをやめていたことでしょう。
麻薬はほどほどにしましょう。
「書く理由」まとめ
まとめましょう。私がブログを書く理由は、
- 文章としてアウトプットしたほうが自分の理解が深まるから
- 数学の面白い話を知ったらみんなに伝えたくなっちゃうから
- ググって出てくるような数学解説はわかりにくいことが多いから
- 承認欲求
基本的には以上の4つです。
これらはとりもなおさず、「あなたが」ブログを書く理由にもなると思います。
誰しも、とは言いませんが、専門分野や興味のある領域の存在する人は少なくないでしょう。
その分野について、全然理解できない! と落ち込むのではなく、ブログに書きましょう。
面白い話を知ったけど忘れてしまいそう……と気を揉むのではなく、ブログに書きましょう。
巷にあふれる解説がわかりにくすぎる!と憤るのではなく、ブログに書きましょう。
承認欲求に関してはいったん忘れましょう。
そんな感じでもって、長いことブログをやってます。鯵坂もっちょでした。
自分のことを書いただけですが、これらの理由付けが皆さんのブログを書くモチベーションにでもつながってくれれば、とても喜ばしいことだと思います。
おわりに
まいったな。「ブログを書く理由」だけで5,000字近くあるとは思わなかったな。別にそんな大層な気持ちで毎回ブログ書いてないんだけどな。
素因数分解の一意性の解説いらないですか?
本当に大丈夫ですか?
しますね。
マイナスでも分数でもない普通の1, 2, 3, 4…という数を「自然数」と呼びますが、すべての自然数はただ一通りに素因数分解ができます。
例えば10なら、28なら
、476568901なら
といった具合です。
「ただ一通りに」というのが大事で、なにか一つの自然数が
などのように2通りに素因数分解されるということはありえません(順番の違いは同じものとみなす)。
これは例えば28はですが実は
でもあるんですよ~ババーン! ということはありえない、ってだけのことを言っています。当たり前ですね。
ごくごく当たり前のことに思えますが、これはそれ自体証明を要する事実であって、つまり全然当たり前ではありません。ちょっと調べてみるとわかりますが、その証明自体も結構大変で、初学者が一朝一夕にできるものではないのです。意外なことです。
で、この「素因数分解がいつもただ一通りにできる」という性質を「素因数分解の一意性」といい、「自然数は素因数分解の一意性を備えている」ということになります。
てことは、素因数分解の一意性とはいつでもかんでも成り立つものではなく、自然数の性質にすぎないんですね。
そうなると「素因数分解の一意性の成り立たないような世界(体系)」もありうるのでは? という問いを立てることができるわけですよ。
3の倍数+1
ここで「3の倍数に1をプラスした数しか存在しない世界」というのを考えてみましょう。
3の倍数とは0, 3, 6, 9, 12, 15, ...なので、つまりこの世界には1, 4, 7, 10, 13, 16, ...という数だけが存在していることになります。
そしてこの世界では、4や10、25などといった数はいわば「素数」のようなものになります。
なぜだかわかりますか? なぜなら、これらの数は「それより小さい数の積に分解できない」からですね。
4、10、25は自然数の上ではそれぞれ2×2、2×5、5×5と素因数分解されますが、今考えている世界には「2」も「5」も存在しません。3の倍数+1の数ではないですからね。
なので"この世界においては"、4や10や25、そして22、34、46なども、それ以上分解できない「素数みたいなもん」になります。
逆に、16、28、40、49などは、この世界においても分解できる合成数です。
これらの数それぞれの"素因数"分解は4×4、4×7、4×10、7×7となり、4も7も10もこの世界に存在しているので分解できる、というわけです。
この「3の倍数+1世界」における素因数分解を一覧にしてみたのが以下です。範囲は1から97まで、「p」はそれ以上「3の倍数+1の数」の積に分解できない"素数"を表します。

さて。ここまでの流れで想像のついている方も多いかもしれませんが、この「3の倍数+1世界」こそ、実は「素因数分解の一意性が成り立たない世界」なのです。
実例を見てみましょう。素因数分解の一意性が成り立たない、その最小の例が「100」です。
100はまず「4×25」と書くことができます。しかし、それに加えて「10×10」とも書くことができるんですね!(それはそう)
前述の通り、4も10も25もこの世界における"素数"です。これはすなわち「100は2通りに素因数分解できる」ことにほかならず、それはまさしく「3の倍数+1世界は素因数分解の一意性が成り立たない体系」であることにほかなりません。
あんなに当たり前かのように思われた素因数分解の一意性も、実は「自然数」という特殊な状況設定があってこそのものだった、ということだったんですね。
この「当たり前だと思ってたことが実は全然当たり前でもなんでもない」というのは数学をやっていると頻繁に発生して、そういう事に気づかせてくれることこそが、数学の魅力の一つだったりもします。
◆
……みたいな感じのことをもうちょっと厳密にして、もう少し高度な話題(モノイドとか)にも触れた記事を今度アジマティクスでやろうと思っていますが、わかりません。怨念の沼底に沈むかもしれません。
というわけで今回は素因数分解の一意性についてのお話でした。数学ってとっても自由でいいですよね。同じくらい、ブログも自由に書けばいいんじゃないかと思います。うまいこと話がつながりましたね。
それでは今回はこのへんで!
著者:鯵坂もっちょ(![]() id:motcho)
id:motcho)

数学ライター&ブロガー。自ら「数学のファン」と名乗り、数学の魅力をさまざまな切り口で伝える。数学好きが集まってダベるだけのイベント「数学デー」支配人。大規模数学イベント「ロマンティック数学ナイト」では、ほかのプレゼンターとは異なる毛色のプレゼンを得意とする。共著に『笑う数学』『笑う数学 ルート4』(共にKADOKAWA)、監修に『OKRA』(正進社)がある。
ブログ:アジマティクス
Twitter:@motcho_tw
同シリーズの過去の記事を読みたい方はこちらから!


